Eine implizite Gleichung ist eine Gleichung, die nicht nach nur einer Variablen aufgelöst ist oder nach eine Variablen aufgelöst werden kann.

Ein Beispiel für eine implizite lineare Gleichung ist

2x + 3y = 1

Diese Gleichung kann nach y aufgelöst werden. Man erhält die explizite Gleichung 

\(y = -\frac{2}{3} x + \frac{1}{3} \)

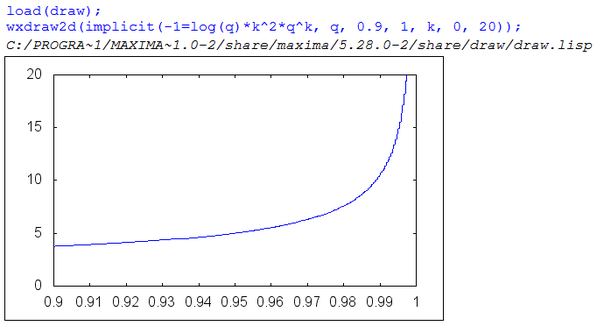
Eine implizite Gleichung, die man nicht nach einer Variablen auflösen kann erhält man z.B., wenn man versucht, optimale Gruppengrößen beim Gruppen-Screening zu bestimmen. Die Gleichung

\(-1 = ln(q) k^2 q^k\)

ist weder nach q noch nach k auflösbar.

Mit einem CAS kann man implizite Gleichungen auf die folgende Art zeichnen:

Zum Kopieren und Einfügen:

load(draw);

wxdraw2d(implicit(-1=log(q)*k^2*q^k,q,0.9,1,k,0,20));

Implizite und explizite Plots können auch in einer Graphik angezeigt werden: