Wie differenziert man mit Maxima?
Um eine (komplizierte) Funktion abzuleiten oder um zu prüfen, ob man eine Ableitung richtig berechnet hat, kann ein CAS hilfreich sein. Mit Maxima geht das folgendermaßen:

Mit
define(Name der Funktion,Term)
legt man zuerst den Namen einer Funktion fest. Mit dem Befehl
diff(Funktionsname,zu differenzierende Variable, Ableitungsgrad)
berechnet Maxima die gewünschte Ableitung. Das berechnete Ergebnis kann jedoch durchaus unübersichtlich sein. Mit
ratsimp(%)
wird das letzte Rechenergebnis (mit "einfachen" Mitteln) vereinfacht. Wie man im Bild oben sieht, ist das hier nicht so erfolgreich gewesen. Mit
radcan(%)
kann Maxima Wurzelausdrücke vereinfachen - viel effektiver, wie man oben sieht!
Differenziert man trigonometrische Funktionen, gewinnt die Art der Vereinfachungsstrategie an Bedeutung. Das folgende Fenster zeigt, dass je nach Vereinfachungsbefehl deutlich unterschiedliche Darstellungsformen entstehen. Wichtig ist, dass man die Wahl hat. Denn ob ein Audruck "einfacher" als ein anderer ist, liegt manchmal im Auge des Betrachters oder ist verbunden mit dem Zweck der Untersuchung:

Wie differenziert man mit Geogebra?
Hier gibt es keine zielgerichtete Möglichkeit einer Vereinfachung des Ergebnisses. Zudem hängt die Schreibweise der "Vereinfachung" von der Art der Eingabe ab. Muss man sich darauf verlassen, dass das Programm den Ausdruck "vernünftig" interpretiert (wie man sieht):
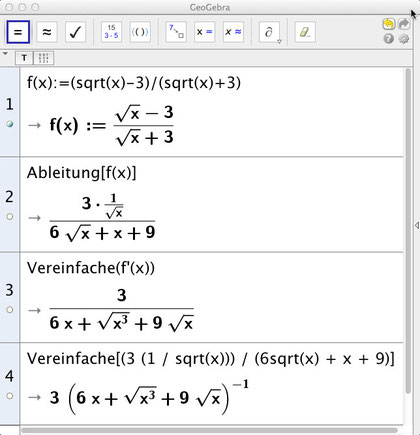
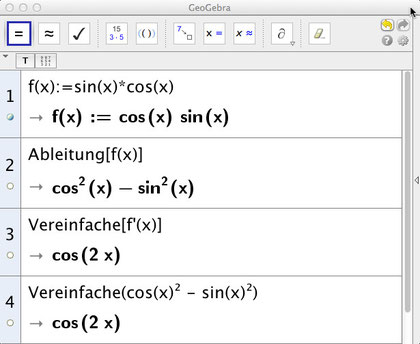
Leitet man mit Geogebra trigonometrische Funktionen ab, so erhält man nur die Ergebnisse, die Maxima mit dem Befehl trigrat() erzeugt. Ob das die "gewünschte" Vereinfachung ist, muss der Anwender entscheiden.
 mathebeimueller:reloaded
mathebeimueller:reloaded